2021国考行测备考：数量关系每年掌握的6大题型

　　一、基本行程问题

　　基本行程问题是较简单的一类行程问题,是围绕着基本公式s=vt展开的,根据题干的情境又可细分为匀速运动型,变速运动型,间歇运动型。

　　(一)匀速运动型核心公式: s=vt;破题点：关于速度、时间或路程的等量关系。

　　(二)变速运动型核心公式: s=vt;破题点:总路程=分段路程之和;总时间=分段时间之和。

　　(三)间隙运动型核心公式: s=vt;破题点：路程等于实际运动时间*速度。

　　【例题】A 地到 B 地的道路是下坡路。小周早上6:00 从A 地出发匀速骑车前往 B 地,7:00 时到达两地正中间的 C 地。到达 B 地后,小周匀速骑车返回,在 10:00 时又途经 C地。此后小周的速度在此前速度的基础上增加1米/秒,较后在 11:30 回到 A 地。问 A.B 两地间的距离在以下哪个范围内?()

　　A.40—50 公里

　　B.大于50公里

　　C.小于 30 公里

　　D.30—40公里

　　【答案】A

　　【解析】步,确定题型。根据题干中“此后小周的速度在此前速度的基础上增加1米/秒”可知,本题属于变速运动。

　　步,分析过程。小周从 A 地到 B 地的过程是匀速的,到中间C地的时候是7:00,所以到B地时应该是 8:00;由此可知,小周由 B 地返回的时间是 8:00,10:00 到达中点C地,故按原速度,小周应该在 12:00 到达 A 地。而在由C 地到 A 地时,小周每秒多骑了 1 米,1 小时就多骑了 3600 米,由C地到A地共花了 1.5 小时,因此共多骑了 3600×1.5=5400(米),这 5400 米按原速度应该花 0.5 小时骑完,因此原速度为(5400÷0.5)米/小时。

　　第三步,计算结果。原计划是 8:00 返回,12:00 到达,可知路程为 5400÷0.5×4=43200(米)=43.2(公里)。

　　因此本题选择 A 项。

　　二、相遇追及问题

　　相遇追及问题是在运动的过程中存在着相遇或者追及，考察的核心是s=vt，只不过这里的s是相遇(追及)路程，v是相对速度(相遇问题是两者速度和，追及问题是速度差)，t是相遇(追及)时间。

　　(一)单次直线型相遇追及问题单次直线型相遇追及问题又可细分为单次线性相遇问题和单次线性追及问题。单次线性相遇问题会在题干中出现“相向”“相遇”字眼，且行程是单次的。所用公式为：相遇距离s=(v1+v2) ×相遇时间t。单次线性追及问题会在题干中出现“追及”字眼,且行程是单次的,所用公式为：追及距离s=(v2- v1)×追及时间t。

　　(二)多次直线型相遇问题

　　甲、乙两人分别从A、B两地同时出发，相向而行，到达对方的出发点之后返回或者甲、乙两人分别从A、B两地同时出发，相向而行，不断往返于A、B之间。出现这样的文字描述，那么就属于直线异地多次相遇问题。

　　结论：从第n-1次到第n次相遇，甲乙的路程和、所用时间、甲的路程、乙的路程均为从出发到次相遇的2倍。

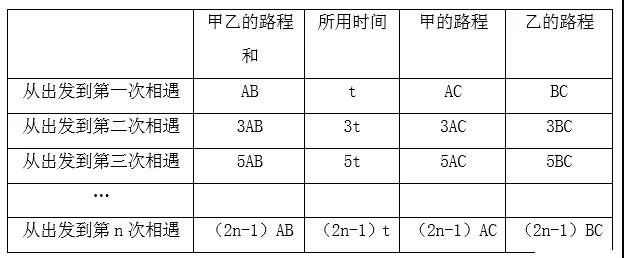
　　结论：从出发到第n次相遇，甲乙的路程和、所用时间、甲的路程、乙的路程均为从出发到次相遇的(2n-1)倍。

　　(三)环形相遇追及问题1、环形相遇环形跑道中的相遇，一般来说都是两个人从同一点出发，方向相反，然后问我们两人之间的相遇问题。要记住基本公式就可以了：环形跑道一周的长=速度和×相遇时间。

　　2、环形追击环形跑道中的追及问题就是封闭路线上的追及问题，关键是要掌握从出发到下次追上的路程差恰好是一圈的长度。也就是环形跑道一周的长= 速度差×追及时间。

　　【例题】甲乙两辆汽车分别从A、B两地沿同一公路同时相向开出，次相遇地点距离A地60千米，相遇后两车继续以原有的速度前行，各自到达B、A后再返回，又在距离B地40千米处相遇，则A、B两地相距( )千米。

　　A.110

　　B.120

　　C.130

　　D.140

　　【答案】D

　　【解析】“相遇后两车继续以原有的速度前行，各自到达B、A后再返回”的文字描述，确定此题为多次相遇问题。根据题目条件已知：从出发到次相遇甲的路程为60千米，又由多次相遇的结论可以得到，从出发到次相遇，甲的路程为(2n-1)*60=180千米，则A、B两地的距离等于180-40=140千米，因此本题选择D项。

　　三、流水行船问题

　　流水行船问题属于行程问题中的一个小的考点，大部分考生对于行程问题的反馈就是这部分太难，考试的时候没有时间做，较终选择放弃，行程问题确实是考试中的一大难题，但是行程问题中的流水行船问题还是比较简单的，如果考生掌握较流水行船的核心公式，就能轻松求解，具体基础知识如下：

　　核心公式：(1)V顺=V船+V水(2)V逆=V船-V水(3)(V顺+V逆)÷2=V船(4)(V顺-V逆)÷2=V水

　　其实公式并不难，难在公式过多，不方便记忆，现在教大家一个小的，让大家可以快速的记住这四个公式，首先我们清楚的一点是，船的速度肯定大于水的速度，二是顺流而下的速度肯定大于逆流而上的速度。所以船的速度就等于(顺流速度+逆流速度)÷2。水的速度就等于(顺流速度-逆流速度)÷2，两个速度相加结果就是大的，除以2就是船的速度，两个速度相减结果就是小的，除以2就是水的速度。

　　【例题】甲、乙两港相距720千米，轮船往返两港需要35小时，逆流航行比顺流航行多花5小时;帆船在静水中每小时行驶24千米，问帆船往返两港要多少小时?

　　A.58

　　B.60

　　C.64

　　D.66

　　【答案】C

　　【解析】我们看到这样的题目要从问题入手，题目让我们求解帆船往返两港口的时间，时间=路程÷速度，路程我们知道，但是速度只知道帆船的速度，我们还需要求出水流的速度，水流的速度我们可以根据轮船的往返进行求解，往返需要35小时，逆行比顺行多花了5个小时，可求顺流时间为15小时，逆流时间为20小时，进而可以求出顺流速度=720÷15=48千米/小时，逆流速度=720÷20=36千米/小时，再根据求水流的速度公式求出水流的速度，水速=(48-36)÷2=6千米/小时，在进行求解帆船的往返时间，时间=720÷(24+6)+720÷(24-6)=24h+40h=64小时。

　　因此本题选择C项。

　　四、时钟问题

　　常考的时钟问题，本质就是追及问题。在表盘上，分针一次又一次追上时钟，一个表盘就是一个360度的圆周。分针跑一圈需要60分钟，这就说明分针每分钟能跑6度;时针跑一圈需要12小时也就是720分钟，说明时针每分钟只能跑0.5度。这就能得出一个速度差了，即分针每分钟比时针多跑5.5度。有了这个基本的知识点，我们就能解决很多问题。

　　【例题】12点20分的时候，时针与分针之间的小夹角是多少度?

　　【答案】110度。

　　【解析】所有人都知道，在12点的时候，时针与分针是重合的，这个时候夹角为零度，但是因为分针比时针跑得快，所以在往后每过一分钟，分针就能甩开时针5.5度，则十分钟时，应该是甩开了5.5×20=110度。所以夹角是110度。

　　五、工程问题

　　工程问题核心公式：工程总量=工作效率×工作时间。

　　方法一：赋值法如果题干给的是单独完成总工作量的时间,此时要对工程总量进行赋值,为方便计算,一般赋工程总量为题干中单独完成总工作量所需时间的较小公倍数。如果题干给出的是效率关系,那就根据比例对它们的效率进行赋值,比如 A、B 的效率比为1：2,那我们就赋 A 的效率为 1,则 B 的效率为 2。

　　方法二：假设法当题干中涉及的具体量不影响较终结果的时候,可以使用赋值法,但当题干中出现了具体的值,且会对结果产生影响的时候,赋值法就显得不是那么好用了。这时可以使用假设法,尽管假设数字可能会与已知条件矛盾,但我们仍然可以强行假设其为某一个数字,然后看看推出的矛盾双方之间的倍数关系，按比例放大或缩小即可。

　　【例题】工程队接到一项工程,投入 80 台挖掘机。如连续施工30天,每天工作 10 小时,正好按期完成。但施工过程中遭遇大暴雨,有 10 天时间无法施工,工期还剩 8 天时,工程队增派 70 台挖掘机并加班施工。问工程队若想按期完成,平均每天需多工作多少个小时?()

　　A. 2.5

　　B. 3

　　C. 1.5

　　D. 2

　　【答案】D

　　【解析】步:本题考查工程问题,考查赋值法;步:赋值每台挖掘机的工作效率为1.根据“正好”得工程总量为 80×30×10=24000。10 天未施工,即是要在剩余的 8 天中干完10+8=18天的工程量。因此 80×18×10=(80+70)×8×t,解得 i=12 小时,因此每天要多干 2 小时。

　　因此本题选择 D 项。

　　六、浓度问题

　　浓度问题，主要指的是在公务员考试中，将涉及到溶液浓度问题的试题称为浓度问题。我们知道溶液会涉及三个量：溶质、溶剂和溶液。

　　1、溶质：被溶解的固体或者液体;2、溶剂：起溶解作用的液体，一般是水;3、溶液：通俗来说，就是将固体或者液体溶解在另一种液体中，得到均匀的混合物。

　　在浓度问题中，主要涉及到的就是这三者之间的关系，通常来说，有以下公式：浓度=溶质/溶液=溶质/(溶质+溶剂)。

　　注意事项：溶液有饱和溶液和不饱和溶液之分，所谓饱和溶液，就是不能再溶解溶质的溶液;不饱和溶液则是指可以继续溶解溶质的溶液。所以我们在答题的时候，要注意溶液是不是饱和溶液。此外，还需要注意，饱和溶液是相对于具体的溶质而言的，如果某种溶液相对于溶质A是饱和溶液，那么这种溶液是不能继续溶解溶质A，但是有可能可以溶解其他溶质。

　　浓度问题答题思路：在解答浓度问题的时候，我们要把握其中的不变量来分析，根据其中的等量关系列出算式，计算解答。通常来说，我们可以以浓度问题的公式为基础，利用列方程、十字交叉、比例、特殊值等方法来解答。一般来说，列方程的方法是较基础的方法，只需要我们找出试题里面的等量关系即可，所以在此我们不做深入的讲解。

　　(一)公式法所谓公式法，就是根据浓度问题的基础公式来解答，在答题的时候，要把握其中的不变量以及变化量，从而能够合理的列出计算式。此外，在采用公式法解答试题的时候，要注意溶液是不是饱和溶液，能不能再继续溶解该种溶质。(二)十字交叉当浓度问题涉及到两种或者两种以上的溶液混合的时候，我们就可以采用十字交叉的方法来分析。假设溶液A、B的质量分别为M、N，浓度为a、b，混合后的浓度为r，则有Ma+Nb=(M+N)r，即M(r-a)=N(b-r)，放入十字交叉模型有：

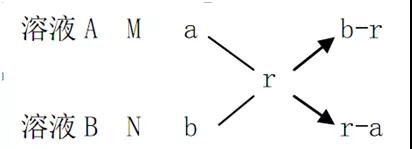
　　从而有M/N=(b-r)/(r-a)。

　　在使用十字交叉方法解答试题的时候要注意以下几点：1、任意两种溶液混合之后，得到的混合溶液的浓度必然在这两个溶液浓度之间，即有a;2、我们在使用十字交叉的时候，如果溶液中加入清水，那么就可以认为清水的溶度为0%，来进行混合。3、当两种溶液的质量相同时，混合得到的溶液的浓度为两种溶液的浓度的平均数，即当M=N时，r=(a+b)/2。

　　【适用类型】当题目中涉及到溶液混合的时候，我们就可以采用十字交叉的方法，从十字交叉的模型可以看出，十字交叉涉及到5个量，所以一般试题会给出其中的3个或者4个量，就可以得到试题答案。