2022-09-05 10:49:53 公务员考试网 
 文章来源:华图教育
文章来源:华图教育
★国家公务员备考资料领取★

添加企业微信领取资料哦
点击查看:2025公务员备考资料推荐
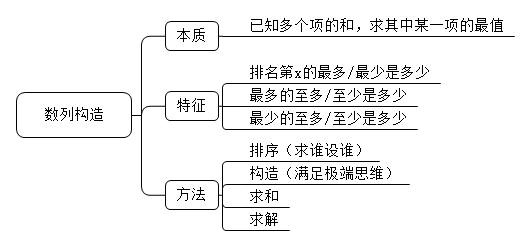
数列构造是公务员数量关系中经常出现的一种题型,是指在数列总和一定的情况下,根据题目的描述,采用极端思维对其他项进行构造,从而对数列中某一项的较大值或最小值进行求解。这类题目的典型特征是在题目最后的提问方式里问:排名第x的最多/最少是多少?最多的至多/至少是多少?又或者最少的至多/至少是多少……同时出现两个“最”,一般都属于数列构造。
那么数列构造如何解决呢?图图今天就教给大家八字秘诀:排序-构造-求和-求解。这第一步就是先排序:对题目中的数列由小到大或者由大到小进行排序,同时题目求哪一项就把哪一项设为x;第二步构造,在满足极端思维的情况下依次去构造别的项;最后列方程求解。
学习了答题之后,我们拿道题目来小试牛刀,一起看下试题吧。
(试题)从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?
A.59B.60
C.61D.62
“问第三重的卡车至少装多少?”这是典型的数列构造题目问法。由题意知,每辆载重各不相同且均为整数,那么一定有大有小。我们先将6辆货车的载重从大到小进行排序:第一重的为71吨,最轻的为54吨。想要第三重的卡车载重最少,则其它货车载重必须尽可能的多,假设第三重的卡车至少载重x吨,依次构造排名第二至第五的载重如下表:
| 排名 | 1 | 2 | 3 | 4 | 5 | 6 | 总计 |
| 载重 | 71 | 70 | x | x-1 | x-2 | 54 | 62×6 |
可列方程:71+70+x+(x-1)+(x-2)+54=62×6,求解得x=60。因此,选择B选项。各位考生只要牢牢掌握八字秘诀:“排序-构造-求和-求解”,就能顺利解决此类题目。数列构造在国考里面也时有出现,我们接着往下看。
(2021年国考市地级第64题)某地10户贫困农户共申请扶贫小额信贷25万元。已知每人申请金额都是1000元的整数倍,申请金额最高的农户申请金额不超过申请金额最低农户的2倍,且任意2户农户的申请金额都不相同。问申请金额最低的农户最少可能申请多少万元信贷?
A.1.5B.1.6
C.1.7D.1.8
“申请金额最低的农户最少申请多少”出现了两个“最”,显然,本题也属于数列构造。首先将10户农户申请金额由高到低进行排序,同时假设申请金额最低的农户最少可能申请x万元信贷,根据“申请金额最高的农户申请金额不超过申请金额最低农户的2倍”,则申请金额最高的农户应申请2x万元,为了避免出现小数,我们统一下单位,25万=250千,要使最低的最低,那么中间8户应尽量高,依次进行构造如下表:
| 排名 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总计 |
| 金额 | 2x | 2x-1 | 2x-2 | 2x-3 | 2x-4 | 2x-5 | 2x-6 | 2x-7 | 2x-8 | x | 250 |
列方程:2x+(2x-1)+(2x-2)+……+x=250,求解得x=15+(千),问最少向上取整,故而最少申请16千,也就是1.6万元信贷。因此,选择B选项。
通过这两道题目不难发现,数列构造特征较为明显,答题套路也相对固定,是各位考生经过一定的练习就能快速拿分的题型。一分耕耘一分收获,图图衷心祝愿各位考生在公考路上披荆斩棘所向披靡!
(编辑:宁夏华图)
10万+
阅读量150w+
粉丝1000+
点赞数